序
这篇文章是CMU 10-414/714的学习笔记第二篇。主要概括课程Lec6-Lec10的内容。本文重点如下,欢迎大家评论补充。
- Initialization: 神经网络的初始化实现
- Optimization: 机器学习优化器实现
Initialization
教授强调了一点:初始化方式会对最终的结果产生非常大的影响,因为模型最终收敛时的参数与初始参数的距离是很小的。我们通常会认为机器学习是一个天资聪颖的神童,只要给他学习资料他就能无师自通;但是事实上模型更像是一个平庸的普通人,终其一生奋斗缺依然逃不了太远。另外,错误的初始化方式还可能会导致下面两个灾难性的结果:
- 如果使用全零的方式初始化参数,亦或是中间某个时刻参数变成了全零,由于 Linear 层梯度和参数是线性的关系(即 dW = X W),梯度也会变成全零,模型至此再无进步的余地。
- 如果使用正态分布来初始化参数,即$W_i \sim \mathcal{N}\left(0, \sigma^2 I\right)$, 那么方差的选择至关重要。方差会影响每一层激活值的大小(准确的来说是norm),进而会影响每一层梯度的大小;更糟糕的是,这个影响会随着模型层数的增加越来越大。过大的方差会导致梯度爆炸,过小的方差则会导致梯度消失。详细的数学论证可以看这个 slides 的第25页,一个基本的结论,合适的方差应该取值:$\frac{2}{n}$,下图则说明了如果方差大于或者大于这个值会导致梯度爆炸/梯度消失。
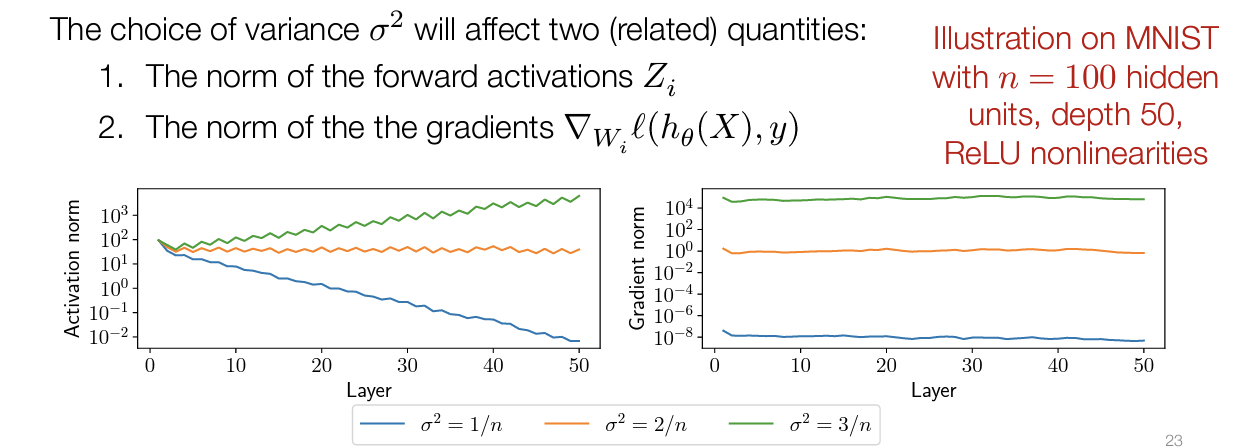
事实上,有很多工作是关于如何初始化参数的。在 hw2中,我们会分别实现下面四种初始化方式。在给定了数学公式之后,用 python 实现起来是非常简单的。
- xavier_uniform and xavier_normal: $a = gain \times \sqrt{\frac{6}{fan_{in} + fan_{out}}}, std = gain \times \sqrt{\frac{2}{fan_{in} + fan_{out}}}$.
- kaiming_uniform: $bound = gain \times \sqrt{\frac{3}{fan_{in}}}, std = \frac{gain}{\sqrt{fan_{in}}}$.
但是,我们其实并不希望初始化方式有这么重要的影响。这里的一个思想就是引入一个新的层来解决这个问题(“fix” the normalization of the activations to be whatever we want.)。下面介绍的两个思想就是解决这个问题:
Layer Normalization LayerNorm 的思想是,既然 activation 会爆炸/消失,那我们就引入一个层来 activation 的均值和方差,让其大小保持在一个合理的范围内。具体公式如下,效果如下图。 \(y = w \circ \frac{x_i - \textbf{E}[x]}{((\textbf{Var}[x]+\epsilon)^{1/2})} + b\)
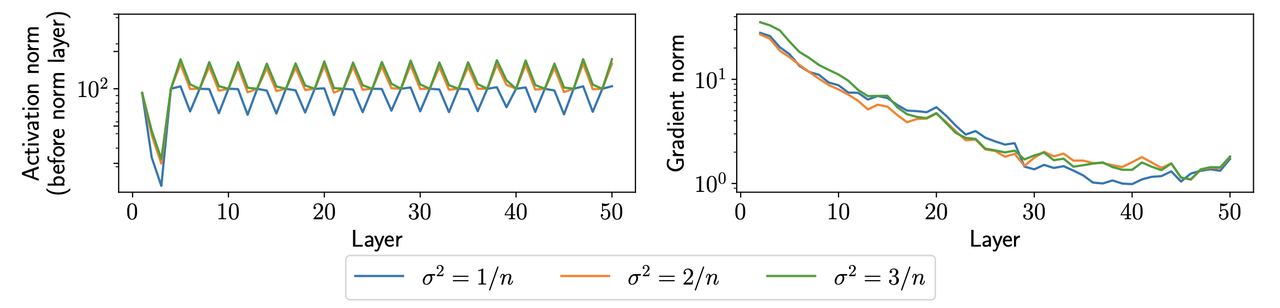
Batch Normalization 还有一个很奇怪的想法是 BatchNormalization 。其采用同 Layer Normalization 的公式,只是均值和方差是 Batch 这个维度的。计算公式如下: $y = \frac{(x - \hat{m}u)}{((\hat{\sigma}^2_{i+1})_j+\epsilon)^{1/2}}$。这里的 $\hat{m}, \hat{\sigma}$ 不是需要计算梯度的参数,仅仅是代表一个需要更新的状态 $\hat{m} = \beta \hat{m} + (1-\beta)\mathbf{E}\left[z\right], \hat{\sigma} = \beta \hat{\sigma} + (1-\beta)\mathbf{Var}\left[z\right], \text{where} \beta is \text{momentum}$.
- 关于 Batch Norm 为什么能 work,目前学术界仍然存在争论。原作者认为其解决了模型参数分布 shift 的问题;一篇论文则认为其让 optimization landscape more smoothly.
- 在hw2的实现中,更新 $\hat{m}, \hat{\sigma}$的过程要注意不引入额外的计算图节点,即应该使用a += b.data 而不是a+=b。
Other normalization
- Group normalization
- instance nomalization
Regularization Regularization的基本思想是限制权重的大小(“limiting the complexity of the function class”),也就是在 loss 里加上 $\frac{\lambda}{2} \sum_{i=1}^D\left|W_i\right|_2^2$。这个在数学上等效于在 optimizer step 的时候加一个 weight decay。证明过程如下: \(W_i:=W_i-\alpha \nabla_{W_i} \ell(h(X), y)-\alpha \lambda W_i=(1-\alpha \lambda) W_i-\alpha \nabla_{W_i} \ell(h(X), y)\)
Optimization
作为一个类,Optimizer 只需要实现一个 step 方法,其会更新模型的参数。下面介绍几个常常见的优化器,最值得关注的是 SGD 和 Adam。
Gradient Descent: $\theta_{t+1}=\theta_t-\alpha \nabla_\theta f\left(\theta_t\right)$,其中 $\alpha$是 learning rate。
SGD: SGD 是 Gradient Descent 的一种变形。基本思想是: Instead of taking a few expensive, noise-free, steps, we take manycheap, noisy steps, which ends having much strong performance per compute. \(\theta_{t+1}=\theta_t-\frac{\alpha}{B} \sum_{i \in B} \nabla_\theta \ell\left(h\left(x^{(i)}\right), y^{(i)}\right)\)
Momentum: 下面公式中的$u_{t+1}$就代表动量(momentum),是一个需要存储的变量: \(\begin{array}{l} u_{t+1}=\beta u_t+(1-\beta) \nabla_\theta f\left(\theta_t\right) \\ \theta_{t+1}=\theta_t-\alpha u_{t+1} \end{array}\)
- 这个公式有一个问题,那就是最开始几步的动量 $u_t$ 是比较小的,因为当前时刻的动量 $u_t$ 有一部分的组成是之前所有时间梯度的加权之和, 最开始的几个动量之前都没怎么算梯度。因此在实践中使用 $\theta_{t+1}=\theta_t-\alpha u_t /\left(1-\beta^{t+1}\right)$来更新参数,来消除这种 bias。 这段话没理解也没关系,反正这个平时也不怎么用。
Adam: 相较于 Momentum, Adam 额外引入了 $v_{t+1}$ 来估计 scale of gradients,其值为梯度平方的级数求和。个人理解这个值代表了梯度的 norm: \(\begin{aligned} u_{t+1} & =\beta_1 u_t+\left(1-\beta_1\right) \nabla_\theta f\left(\theta_t\right) \\ v_{t+1} & =\beta_2 v_t+\left(1-\beta_2\right)\left(\nabla_\theta f\left(\theta_t\right)\right)^2 \\ \theta_{t+1} & =\theta_t-\alpha u_{t+1} /\left(v_{t+1}^{1 / 2}+\epsilon\right) \end{aligned}\)
附录
- 除了上面提到的实现,hw2中还会让我们实现 Linear, ReLU 等非常基本的网络层。事实上这些层都是基于我们在hw1中实现的 Tensor 和 Op 来实现的,当你学会了搭建这些基本的层之后,就可以自己搭建一个小型的 MLP 了。MLP 足够解决 Cifar10,这也是 hw2 的最终目标:从头搭建一个能解决。
- slides 中还提到了另一种求解最优梯度的办法:牛顿法(Newton’s method): $\theta_{t+1}=\theta_t-\alpha\left(\nabla_\theta^2 f\left(\theta_t\right)\right)^{-1} \nabla_\theta f\left(\theta_t\right)$。理论上这个方法可以更快的收敛到最优解,但是计算Hessian矩阵( $\nabla_\theta^2 f\left(\theta_t\right)$ )太慢了;另外对于 non-convex optimization, 我们其实不确定我们是否想要往局部最优解的那个方向走。
- 类似牛顿法,Nesterov Momentum法是一种理论上可以更快的逼近局部最优解的更新方法: $u_{t+1}=\beta u_t+(1-\beta) \nabla_\theta f\left(\theta_t-\alpha u_t\right)$。其本质是使用 gradient of next point来更新 momentum,这个可以加速凸优化问题的求解,但是在 Deep Learning 的场景下不一定有用。