背景
先来看看原题: (懒得看英文的小伙伴没关系，后面会有中文概括，但建议还是看看原题)
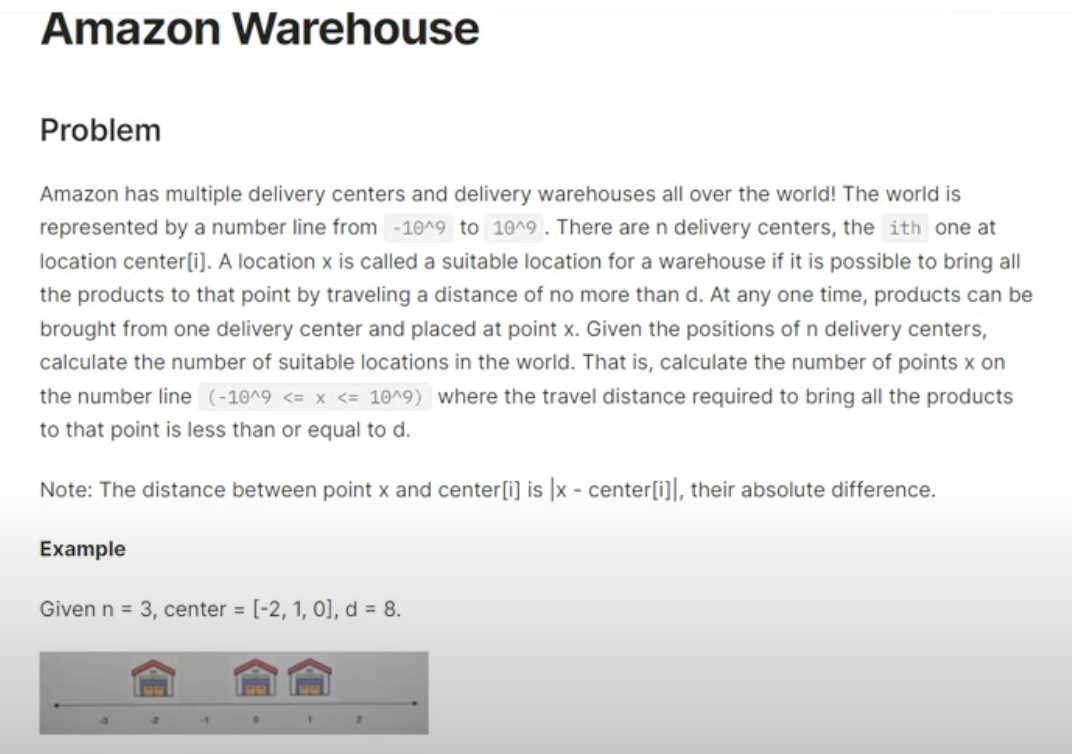
注: 图片来自这个人的YouTube视频: https://www.youtube.com/watch?v=aPP8wkSBiLg, 评论区的链接不知道为啥打不开了，因此我放了截图，这个是我看到的对这道题目最完善的描述，很遗憾他提供的代码不是最优雅的。其他题目链接可以参考这个链接和这个链接。可以看出这是一道高频出现的OA题，只是网上似乎没有正确的做法，因此今天写一个笔记来讲讲这道题的思路。
总结一下就是，在一条线上有N个亚麻仓库，每个点有个坐标a[i]，我们的目标是建一个送货站x，要求x到这N个点的Travel distance小于等于D(D是题目的输入)，其中travel distance的定义是 2 * abs(x - a[i])，代表从送货站到仓库再会送货站的距离，问总共有多少个整数坐标满足这个条件；
暴力解法
凡是做题，我们第一步一定是先想到一个正确的做法，管他超不超时。这道题的一个暴力解法就是对平面上所有可能的坐标进行遍历(题目里给了坐标的范围是[-1e9, 1e9]，所以我们是能枚举所有的点的)，计算每个点到N个仓库之间的距离，在乘以2，判断是否小于D。代码如下。当然，计算每个点到N个仓库的距离耗时O(N), 这个做法时间复杂度 O(2e9 * N)，必超时。
1
2
3
4
5
6
7
8
9
10
11
12
13
MAX_N = int(1e9)
def calculate_distance(a, x, n):
dist = 0
for i in range(n):
dist += abs(a[i] - x)
return dist
def solution(a, n, d):
count = 0
for x in range(a[0] - d, a[-1] + d + 1):
if calculate_distance(a, x, n) * 2 <= d:
count += 1
return count
不优雅的二分解法
网上很多解法都说要binary search，这个想法倒确实非常自然。因为时间复杂度起码能降低到 O(log(1e9) N) = O(31N)。对这道题来说是不会超时的。但是如果这是一道面试题,我是面试官，你给我说要遍历所有的点，这件事情本身就很奇怪。因此我认为这个解法是不够优雅的。当然本身网上很多二分的解法就是错的。
从原理上来说，二分有一个很强的要求，那就是得有东西是单调有序的。这样才能保证通过中点的状态快速过滤一半的区间。在这个例子里，定位F(x)代表x到N个仓库之间的距离，F(x)是一个先递减再递增的函数，对这种函数用二分是有问题的。如果用二分的时候，F(mid) > d，这种时候应该去左区间找答案还是去右区间找答案呢？下面两张图，一张图的答案在左区间，一张图的答案在右区间。
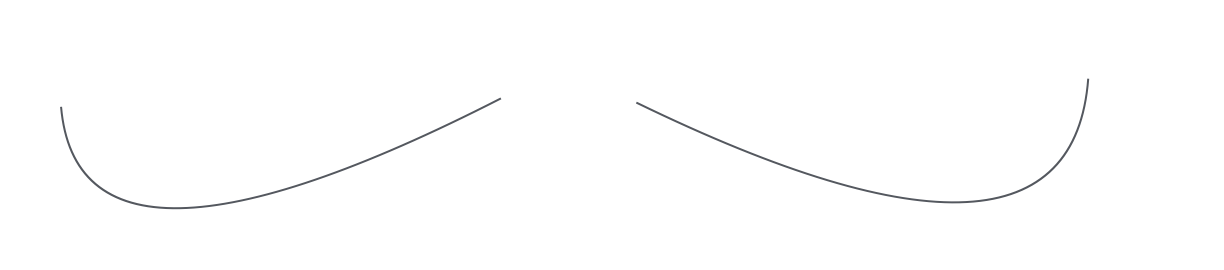
如果要使用二分，那么就必须找到函数F的最低点。只有这样我们才能找到两个单调的区间。这里就需要用到一些数学知识: 对于一个线段，这个线段里的所有的点到这个线段的两个端点的距离都是一样的，且是最小的。也就是说，如果N是奇数，F取到最小值的点就是a[N//2]；如果N是偶数，N是偶数，F取到最小值的点就是[ a[N//2-1], a[N//2] ]这个闭区间。也就是说，不管怎么样，a[N//2]这个点都是一个最值点。注: 我们可以假设数组a是有序的，这个只需要对输入进行一次排序就可以了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 在[left, right]这个区间内，找到一个最大的区间，使得其中的点都满足2*F(x) <= d
# 对于单调递增函数, 要找到最大的right
def binary_check_for_mono_increase(left, right, a, n, d):
ans = left
while left <= right:
mid = (left + right) // 2
if calculate_distance(a, mid, n) * 2 <= d:
ans = max(ans, mid)
left = mid + 1
else:
right = mid - 1
return ans
# 对于单调递减函数, 要找到最小的left
def binary_check_for_mono_decrease(left, right, a, n, d):
ans = right
while left <= right:
mid = (left + right) // 2
if calculate_distance(a, mid, n) * 2 <= d:
ans = min(ans, mid)
right = mid - 1
else:
left = mid + 1
return ans
def solution(a, n, d):
lowest_point = a[n//2]
if calculate_distance(a, lowest_point, n) * 2 > d:
return 0
left_bound = binary_check_for_mono_decrease(-MAX_N, lowest_point, a, n, d)
right_bound = binary_check_for_mono_increase(lowest_point, MAX_N, a, n, d)
return right_bound - left_bound + 1
咱就是说这个代码绝对比YouTube视频里的代码要好。这个代码虽然也是 O(N)的代码，但是由于常数项很大，依然有超时的风险。
区间
整体思路: 我们把整个区间分成 [ MIN_INT, MAX_INT ], [ a[0], a[N-1] ], ... [ a[N//2-1], a[N//2] ] 这 N 个区间，之所以这么划分:
- 对于一段区间，如果这段区间的两个端点都满足
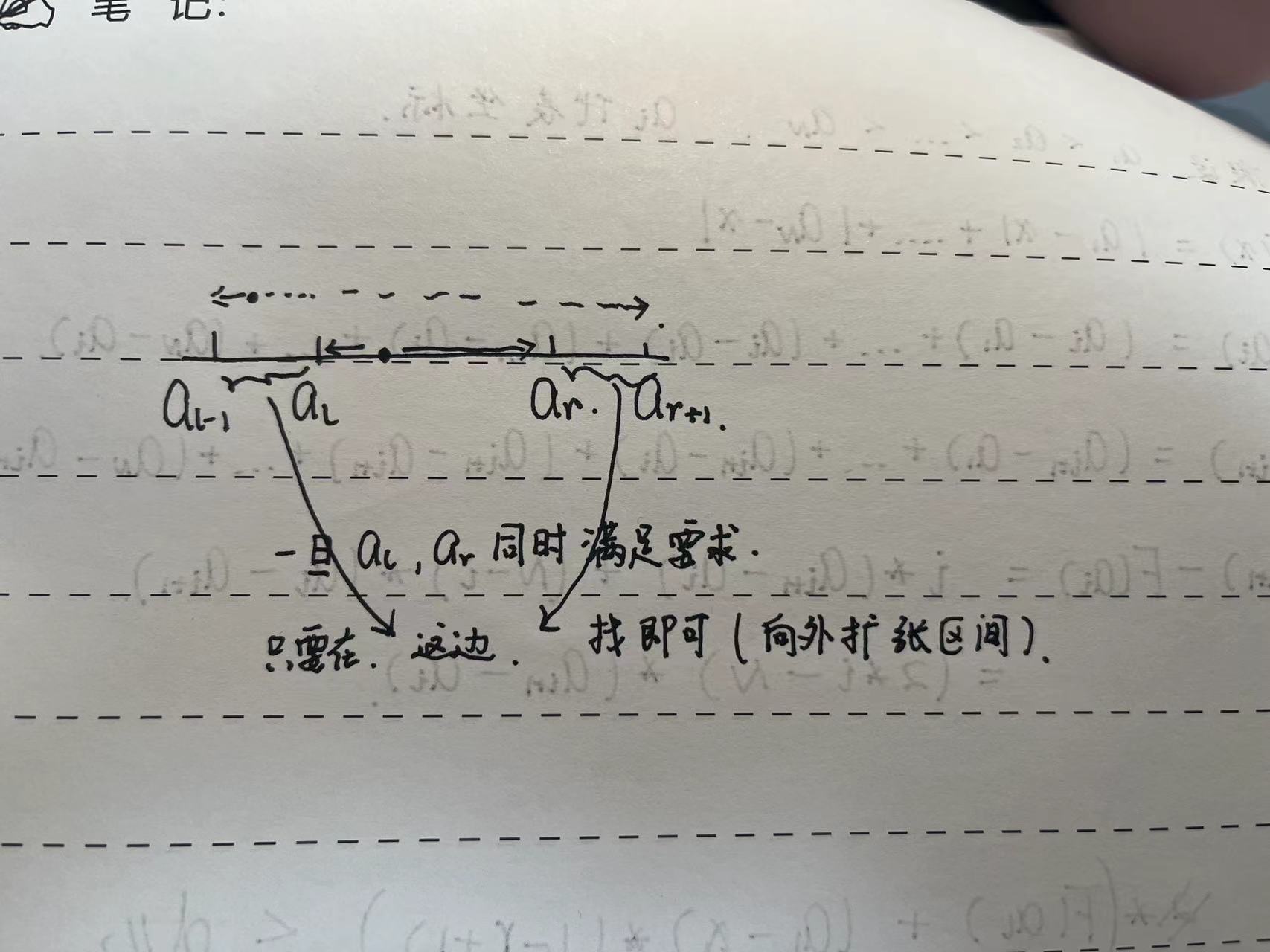
2 * F(x)<= d, 那么这段区间里的每一个点必然都满足要求，因为这个函数是一个向下凹的函数。我们只需要考虑怎么往外扩就好了。 - 之所以这么两两分组，就是方便”往外扩”。如果
a[l], a[r]这个区间内的点到a[0], a[N-1]的距离之和是一样的， 到a[1], a[N-2]的距离之和是一样的，，他们只有到a[l+1], ..., a[r-1]这些点的距离之和不一样。 - 对于
a[l]左边的x，F(x) = F(a[l]) + (l-r+1)*(a[l]-x), 求解F(x) <= 2*d, 得到x >= a[l] - (d//2-F(a[l]))/(l-r+1) - 类似的，对于
a[r]右边的x，F(x) = F(a[r]) + (l-r+1)*(x-a[r])，求解F(x) <= 2*d, 得到x <= a[r] + (d//2-F(a[r]))/(l-r+1)
如何快速计算 F(a_i)
\(\begin{aligned}
F(x) &= |a_0 - x| + ... + |a_{N-1} - x| \\
F(a_i) &= (a_i - a_0) + ... + (a_i - a_0) + (a_{i+1} - a_i) + ... + (a_{N-1} - a_i) \\
F(a_{i+1}) &= (a_{i+1} - a_0) + ... + (a_{i+1} - a_i) + (a_{i+1} - a_{i+1}) + ... + (a_{N-1} - a_{i+1}) \\
F(a_{i+1}) - F(a_i) &= (i+1) * (a_{i+1} - a_{i}) + (N-i-1) * (a_{i} - a_{i+1}) \\
&= (2*(i+1) - N) * (a_{i+1} - a_{i})
\end{aligned}\)
考虑到我们需要O(N)的时间计算F(a[1])，再需要O(N)的时间遍历数组，因此计算这N个数字的时间复杂度是O(N)的。
你是不是完全没有听懂呢？没关系，反正下面这段代码是对的。
1
2
3
4
5
6
7
8
9
10
11
12
13
def solution3(a, n, d):
F = [calculate_distance(a, a[0], n)]
for i in range(n-1):
F.append( (2*(i+1) - n) * (a[i+1] - a[i]) + F[i] )
l, r = 0, n-1
while l <= r:
if 2*F[l] <= d and 2*F[r] <= d:
break
l += 1
r -= 1
if l > r:
return 0
return a[r] - a[l] + 1 + (d//2-F[r])//(r - l + 1) + (d//2-F[l])//(r - l + 1)
